ILE Math Bindable API Descriptions

The following information is provided for each math bindable API.

Definition
This column states the nature of the computation performed by the API.

API Name
This column gives the API names of the procedure.

Parameter Type
This column describes the acceptable parameter types that are input to and output by the specified API, and is indicated by the following characters:
I 32-bit binary integer.
J 64-bit binary integer.
S 32-bit single floating-point number.
D A 64-bit double floating-point number.
T A 32-bit single floating-complex number (both real and imaginary parts are 32 bits long).
E A 64-bit double floating-complex number (both real and imaginary parts are 64 bits long).

Note: The characters correspond to the fifth character of the called API.

Equation
This column gives a math equation that represents the computation.

The following notation is used in the equations of the APIs:

|x| denotes the absolute value of x.
sign(x) is +1 if x >= 0 or -1 if x < 0.
f denotes a function result.
z denotes a complex argument, where 
z = x + iy.
z1 and z2 denote two complex arguments, where 
z1 = x1 + iy1 and z2 = x2 +iy2.
No. Inputs
This column states how many input parameters must be passed to the routine. See Calling Math Bindable APIs for a description of the format of APIs with 1 or 2 input parameters.

Input Range
This column gives the valid range for input parameters. If a parameter is not within the range, an error message is issued. (See the table below for a description of the messages that can be generated by the math bindable APIs.)

For output ranges, see Data Types and Limits for information concerning integer data types, real data types, and complex data types.


Math API Descriptions


  Service Program Name: QLEMF

  Default Public Authority: *USE

  Threadsafe: Yes

Definition API Name Para- meter Type Equation No. Inputs Input Range1
Absolute Function CEESxABS I
J
S
D
T
E
 f = |x|
or
f = |z|
1 Any integer number (for parameter type I and J).

Any real number (for parameter types S and D).

Any complex number (for parameter types T and E).
Arccosine CEESxACS S
D
f = cos-1(x)
 1 |x| <= 1
Arcsine CEESxASN S
D
f = sin-1(x)
 1 |x| <= 1
Arctangent CEESxATN S
D
T
E
f = tan-1(x)
or
f = tan-1(z) = tan-1(x + iy)
1 Any real argument (for parameter types S and D).

Any complex argument (for parameter types T and E).
Arctangent2 CEESxAT2 S
D
f = atan2(y/x)

For x > 0,
atan2(y, x) = tan-1(y/x).

For x < 0 and y > 0,
atan2(y, x) = pi + tan-1(y/x).

For x < 0 and y < 0,
atan2(y, x) = -pi + tan-1(x/y).
2 y is not equal to 0.0 and
x is not equal to 0.0;

y is not equal to +INF or -INF and
x is not equal to +INF or -INF
Conjugate of Complex CEESxCJG T
E
f = x - iy for argument z = x + iy.
 1 Any complex number.
Cosine CEESxCOS S
D
T
E
f = cos(x)
or
f = cos(z) = cos (x + iy)

 1 Any real argument, in radians, such that
|x| <= 0x432921FB54442D18 ~= pi * 250
~= 3537118876014220.0.
Any complex number such that
|y| <= 88.7228 for FLOAT4 and
|y| <= 709.7827 for FLOAT8,
and x is any real argument.
Cotangent CEESxCTN S
D
 f = cot(x)
 1 Any real argument, in radians, such that
|x| <= 0x432921FB54442D18 ~= pi * 250
~= 3537118876014220.0.
Error Function and its Complement CEESxERF CEESxERC S
D

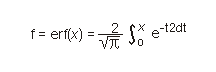
f equals error function of x equals 2 divided by the square root of pi multiplied by the integral from 0 to x of e raised to minus t squared times d t

 1 Any real argument
Exponential Base e CEESxEXP S
D
T
E
f = ex
or
f = ez = ex+iy
1 -87.3365 <= x <= 88.7228
(for parameter type S).
-708.3964 <= x <= 709.7827
(for parameter type D).
-87.3365 <= x <= 88.7228 and y is any
real number (for parameter type T).
-708.3964 <= x <= 709.7827 and y is
any real number where
|y| <= 0x432921FB54442D18 ~= pi * 250
~= 3537118876014220.0.
(for parameter type E).
Exponentiation CEESxXPy I
J
S
D
T
E
f = xy (See note 2)
 2 Any integer arguments (for CEESIXPI, CEESSXPI, CEESDXPI, CEESTXPI, CEESEXPI, CEESJXPJ, CEESSXPJ, CEESDXPJ, CEESTXPJ, CEESEXPJ).

Any real argument subject to the condition that if x is negative, y must be an integer (for CEESSXPS, CEESDXPD).

For complex data types, see the argument for real data types above (for CEESTXPT, CEESEXPE).
Factorial CEE4SxFAC I
J
n! = 1*2*3 ... (n-1)*n.
 1 For parameter type I, any integer <=12. For parameter type J, any integer <=20.
Floating Complex Divide CEESxDVD T
E
f = z1 / z2 = (x1 + iy1) / (x2 + iy2)
 2 Any complex number.
Floating Complex Multiply CEESxMLT T
E
f = z1 * z2 = (x1 + iy1) * (x2 + iy2)
 2 Any complex number.
Gamma Function CEESxGMA S
D

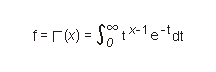
f equals gamma function of x equals integral from 0 to plus infinity of t raised to x minus 1 multiplied by e raised to minus t multiplied by d t

 1 0 < x <= 35.04
(for parameter type S).
0 < x <= 171.6243
(for parameter type D).
Hyperbolic Arctangent CEESxATH S
D
T
E
f = tanh-1(x)
or
f = tanh-1(z) = tanh-1(x + iy)
1 Any real argument such that

|x| <= 1
(for parameter types S and D).
Any complex number such that
x is not equal to 1.0 and y is not equal to 0
(for parameter types T and E).
Hyperbolic Cosine CEESxCSH S
D
T
E
f = cosh(x)
or
f = cosh(z) = cosh(x + iy)
1 Any real argument such that
|x| <= 89.4159 (for FLOAT4)
and |x| <= 709.7827 (for FLOAT8).
Any complex number such that
|x| <= 89.4159 (for FLOAT4)
|x| <= 709.7827 (for FLOAT8).
Hyperbolic Sine CEESxSNH S
D
T
E
f = sinh(x)
or
f = sinh(z) = sinh(x + iy)
1 Any real argument such that
|x| <= 89.4159 (for FLOAT4)
and |x| <= 709.7827 (for FLOAT8).
Any complex number such that
|x| <= 89.4159 (for FLOAT4)
and |x| <= 709.7827 (for FLOAT8).
Hyperbolic Tangent CEESxTNH S
D
T
E
f = tanh(x)
or
f = tanh(z) = tanh(x + iy)
1 Any real argument
(for parameter types S and D).
Any complex number such that
|x| < 43.66825 (for parameter type T),
and |x| < 354.1982
(for parameter type E).
Imaginary Part of Complex CEESxIMG T
E
f = y, where z = x + iy.
 1 Any complex number.
Log Gamma Function CEESxLGM S
D
f = ln(Gamma (x))
 1 0 < x <= 4.0850*1036
(for parameter type S),
and 0.0 < x <= 21014
(for parameter type D).
Logarithm Base 10 CEESxLG1 S
D
f = log10(x)
 1 x > 0.0
Logarithm Base 2 CEESxLG2 S
D
f = log2(x)
 1 x > 0.0
Logarithm Base e CEESxLOG S
D
T
E
f = loge(x)
or
f = ln(z) = loge(|z|) + iatan2(y, x)
1 x > 0.0 (for parameter types S
and D).
z is not equal to 0+i0 (for parameter types T
and E).
Modular Arithmetic CEESxMOD I
J
S
D
f = remainder of x/y (See note 3)
 2 Any two integer numbers such that
y is not equal to 0 (for parameter types I and J).
Any two real numbers such that
y is not equal to 0.0 (for parameter types S
and D).
Nearest 64-Bit Integer CEESxNJN S
D
If x >= 0.0
f = sign(x)*n
where n is the largest 64-bit integer
<= |x + 0.5|
or
If x < 0.0
f = sign(x)*n
where n is the largest 64-bit integer
<= |x - 0.5|
1 Any real number.
Nearest Integer CEESxNIN S
D
If x >= 0.0
f = sign(x)*n
where n is the largest integer
<= |x + 0.5|
or
If x < 0.0
f = sign(x)*n
where n is the largest integer
<= |x - 0.5|
1 Any real number.
Nearest Whole Number CEESxNWN S
D
If x >= 0.0
f = sign(x)*n
where n is the largest integer
<= |x + 0.5|
or
If x < 0.0
f = sign(x)*n
where n is the largest integer
<= |x - 0.5|
1 Any real number.
Positive Difference CEESxDIM I
J
S
D
If x > y, f = x - y
or
If x <= y, f = 0
2 Any integer argument
(for parameter types I and J).
Any real number
(for parameter types S and D).
Sine CEESxSIN S
D
T
E
f = sin(x)
or
f = sin(z) = sin(x + iy)
1 Any real argument, in radians, such that
|x| <= 0x432921FB54442D18 ~= pi*250
~= 3537118876014220.0
(for parameter types S and D).
Any complex number such that
|y| <= 88.7228 (for parameter type T),
and |y| <= 709.7827, and
|x| <= 0x432921FB54442D18 ~= pi*250
~= 3537118876014220.0
(for parameter type E).
Square Root CEESxSQT S
D
S
D

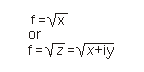
f equals the square root of x or f equals the square root of z where z is a complex number

 1 Any real argument such that x >= 0.0
(for parameter types S and D).
Any complex number such that
|z| + |x| <= 1.797693*10308
(for parameter types T and E).
Tangent CEESxTAN S
D
T
E
f = tan(x)
or
f = tan(z) = tan(x + iy)
1 Any real argument, in radians, such that
|x| <= 0x432921FB54442D18 ~= pi*250
~= 3537118876014220.0
(for parameter types S and D).
Any complex number such that
|y| < 43.66825 (for parameter
type T), and |y| < 354.1982
(for parameter type E).
Transfer of Sign CEESxSGN I
J
S
D
f = sign(y)|x|
 2 Any integer argument
(for parameter types I and J).
Any real number
(for parameter types S and D).
Truncation CEESxINT S
D
f = sign(x)*n,
where n is the largest integer
<= |x|
1 Any real number.
Notes:
1
For output ranges, see Data Types and Limits, including information on Integer Data Types, Real Data Types, and Complex Data Types.
2
Where x and y have the following combinations, respectively: 
integer, integer
real FLOAT4, integer
real FLOAT8, integer
single complex, integer
double complex, integer
real FLOAT4, integer
real FLOAT8, integer
single complex, integer
double complex, integer
64-bit integer, 64-bit integer
real FLOAT4, 64-bit integer
real FLOAT8, 64-bit integer
single complex, 64-bit integer
double complex, 64-bit integer
real FLOAT4, real FLOAT4
real FLOAT8, real FLOAT8
single complex, single complex
double complex, double complex
3
The absolute value of the result is always less than the absolute value of y.


Top | ILE CEE APIs | APIs by category